Visualizations and Analysis of the 2009 Iranian Election

Several people have now been analyzing the Iranian election results for evidence of fraud. I started following this as it developed, and wanted to present the arguments in a more understandable way--both through text and visualization. In particular, Professor Walter Mebane of the University of Michigan was very helpful in making data available and providing a rich set of analyses to consider. What follows is visualization and explanation of others' analysis, shaded by my own impression of its strength. Note that this is not arguing about who should have won the election, or even whether there was fraud in the election: instead, it is analyzing the arguments about whether there is convincing statistical evidence of fraud in the election returns. In fact, the strongest evidence of possible fraud may be non-statistical, in the report here by Professor Ali Ansari, Daniel Berman, and Thomas Rintoul (all from Chatham House/St. Andrews).

Data

The data analyses presented here are performed on three levels of ballot aggregation: polling station (or "ballot box")-level data; district (ot town) level data; or province-level data. The ballot-box and district-level data were made available by Professor Mebane (though the original source is the Iranian government itself, here). This data has been organized directly into csv form and made available below. Town-level data from 2005 was also made available by Professor Mebane, and is available below.

There are 320 towns, from 30 provinces. Basic data include the number of votes for Ahmadinejad, number of votes for Mousavi, and number of invalidated ballots. Most districts report 60-90% voting for Ahmadinejad.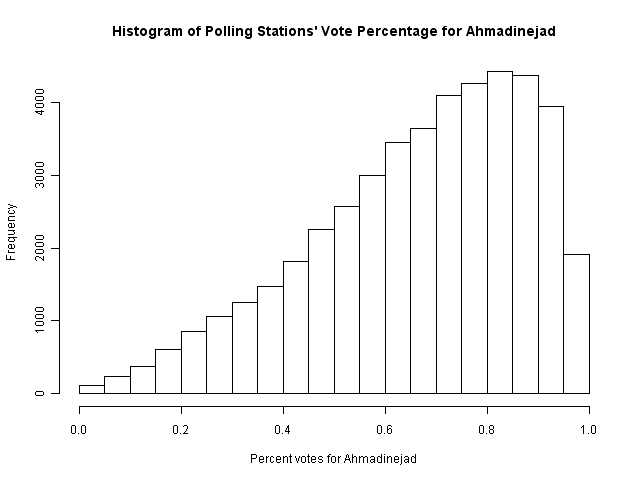

Data files

All files (including data and graphs) are contained in iranian_election.zip. The r file to replicate the analysis is visualize_Iran.r, which uses the multinomRob package (available at CRAN) and the R files HelperFunctions.R, Benford.R, and Models.R. The subdirectory collateData contains the source data files and script used to collate these into the combined csv files.

The data files are:

Note that there is some discrepancy in the totals between the ballot box, precinct, and province totals, due to the fact that the ministry has released multiple versions (updates/corrections) of the election results data.

Professor Mebane's notes and files are at http://www-personal.umich.edu/~wmebane/. Most of the visualizations here are directly of his work, and would not be possible without his data and program files.
Files for Beber and Scacco are at http://www.columbia.edu/~bhb2102/

Is Something Strange in the 1st Digits? (Roukema)

Boudewijn Roukema has come up with an analysis of the district-level data at http://arxiv.org/PS_cache/arxiv/pdf/0906/0906.2789v3.pdf. Dr. Roukema suggests that the excess of vote counts starting with the digit '7' for Karoubi is sufficient to indicate fraud. The argument is that if you look at the total ballots for each candidate by province, and just look at their first digits, then they should follow a pattern called Benford's Law. You can find an introduction to Benford's law here. What it says is that there will be more counts which start with the digit 1 than with 2, more with 2 than with 3, and so on. You can even figure out how many you would expect to begin with each digit. This distribution is very interesting, and holds true for a large variety of data, including even mathematical constants found in nature. Benford's Law is now commonly used to look for financial fraud--when changing counts, people have trouble acting randomly, and this is one way to detect that. But it does not hold for all data, and it is not clear that election data follows Benford's distribution. For example, the Carter Center's Report on the Venezuelan election, in which they investigate claims of fraud, states that election results in general will not conform to Benford's law.

However, if we assume that the district-level data should follow Benford's law, then we can see how well Benford's law fits. If the numbers are very different from what we expect, this indicates that the data were created in some other way, which would indicate fraud. The statistical test for this is the Chi-squared test, essentially testing how often we might get a result like this due to chance.

So let's look at this. The p-value is for a Chi-square binning test for all digits.

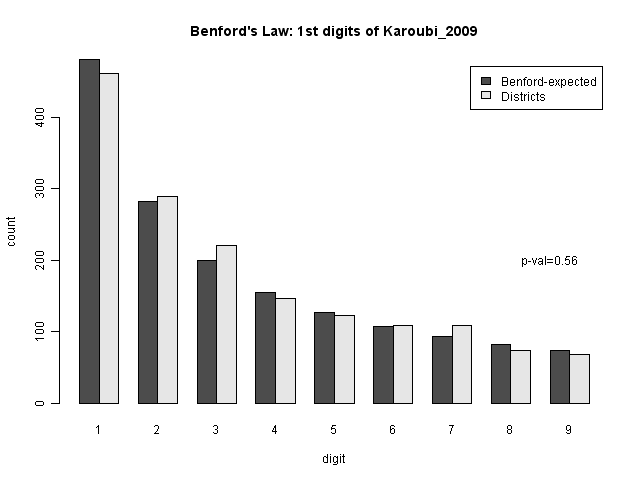
We can see that from the overall numbers, it doesn't look that different from what Benford's law would predict. In fact, we have a p-value of 0.56, which is about as normal as you can get.

Now, what Roukema does is look only at the results for one of the candidates, Karoubi. If we look only at the district-level data for Karoubi, we see the following:

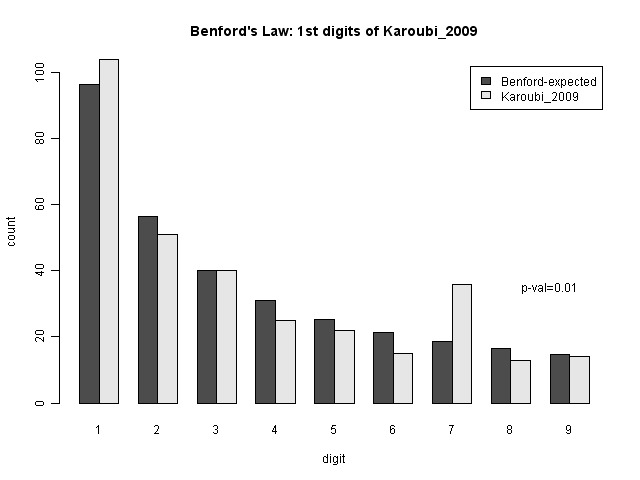
Roukema uses a Poisson test of the 7-digit in isolation; the justification for this is not entirely clear to me.

This single anomaly, for a candidate who is not one of the leading two, does not seem to be strong evidence of fraud. It is difficult to determine what fraudulent action might be taken to have caused this single-digit anomaly in a minor candidate; if numbers were fabricated, we would expect to see a similar pattern over all candidates. Nate Silver and Andrew Gelman both make cases against this conclusion at fivethirtyeight.com. However, I do recommend the paper for its technical discussion of Benford's law in theoretical and empirical form.

Now, a Chi-squared test on Karoubi does come up with a low p-value. However, we cannot consider that p-value in isolation. Because we are looking at multiple possible deviations, we must consider the issue of multiple testing.

The main idea of multiple testing corrections is that when we are looking at lots of tests, or lots of data sets, it's more likely tht we would find something statistically unusual, just because we are looking at more possibilities. Put simply, if something has a 1-in-100 chance of happening, but we look at 100 different times where it could happen, we actually have a pretty good chance of seeing one. The same holds, to a lesser extent, when we are considering five possibilities.

There are five different district-level numbers we could look at: number of invalid votes, votes for Ahmadinejad, votes for Mousavi, votes for Rezaei, and votes for Karoubi. So to have a 1-in-100 chance of happening in any of these, we would normally be looking for a p-value of 0.01/5=0.002. (This is something called the Bonferroni correction. It ensures that we do not treat things as significant more often than we should, but is also known to be conservative: it will more often reject things which are truly significant. There are less conservative corrections.)

Finally, Benford may not hold for Karoubi's results in particular, because the counts are centered around one scale. Benford's law only holds if the data span several

We can see this in histogram distributions of Karoubi's vote totals over the 320 districts. A simple histogram shows that most are in the region of 100 to 1000, with some in 10-100 and 1000-10000.

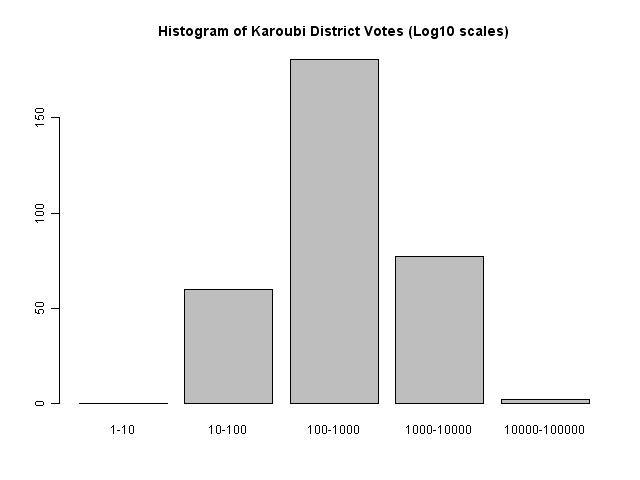
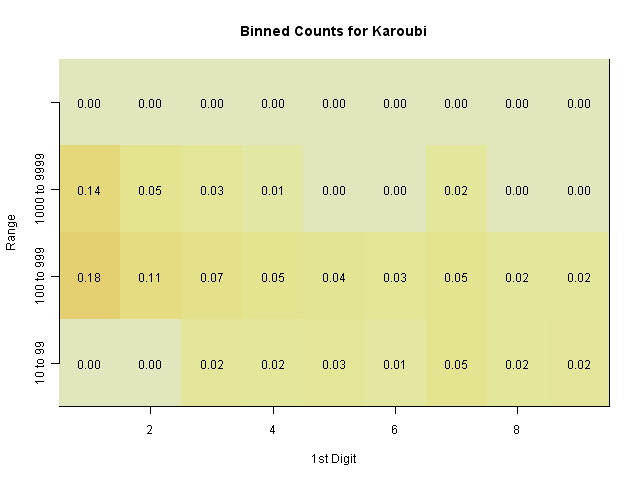
This might be okay; but if we look more closely, we can see that the data does not really span the whole 10-100 or 1000-10000 range. Instead, it is centered around that 100-1000 range: most of the values from 10-100 are near 100, and most of the values from 1000-10000 are near 1000. This means that it doesn't even really span three orders of magnitude. We can see this in the following plot:


Each box shows the proportion of the 320 provinces which fall into this range, and have this first digit. We can see that most of the values in the 10-100 range have a first digit 3-9 (i.e., 30-99) rather than 10 or 20.

Because of this, Benford's distribution cannot be expected to hold.

Is Something Strange in the 2nd Digits? (Mebane)

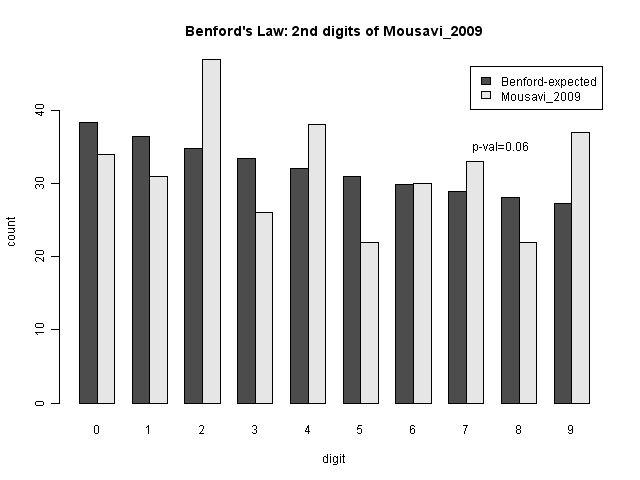
Professor Mebane looked at using Benford's law on the 2nd digits of each of the vote counts, both for ballot-box level and district level counts. The second distribution also follows Benford's law, but with a slightly different distribution of digits. He says that there are many elections where Benford's law does not hold for the first digit, but does for the second.

Each of the following graphs shows the expected number of values with the given second digit under Benford's Law, and the actual numbers from the data. The p-value is a measure of how likely, if Benford's Law is followed, one might get these values (or more extreme ones) just by chance. A low p-value would indicate a very unusual (improbable) result; traditionally, p-values below 0.05 are considered significant.

The results are not significant for the number of votes for Mousavi, but are significant for the number of votes for Ahmadinejad. As we can see from the bar chart comparisons, there are many more 0's than expected (and to some extent other differences as well).

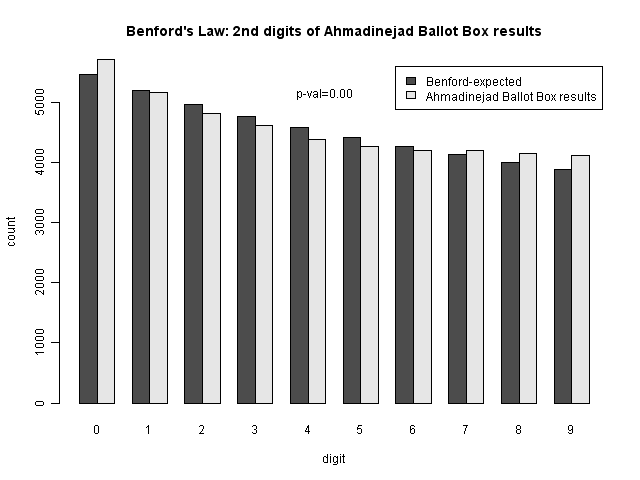
This seems to be a real pattern (the digit variation is smooth, suggesting that it's not simply a single anomaly like the sevens digit. The question is whether or not it is evidence of fraud. Professor Mebane considers this to be strong evidence of fraud in the election. One way to check that would be to determine what type of fraudulent activity which would create this pattern. But another possibility is that the sizes of the ballot boxes (which are intended to cover a certain number of people) could have caused this effect. Looking at a heatmap of the range of values of votes at the ballot box level, we can see that they are fairly tightly constrained to the 100-1000 range.


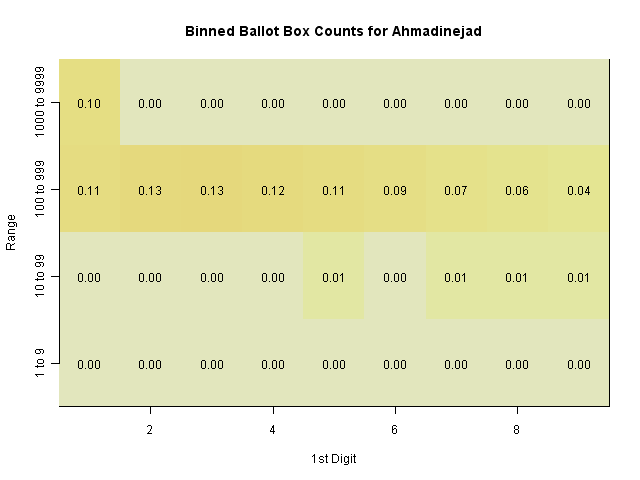
Each box shows the proportion of the 45692 ballot boxes which fall into this range, and have this second digit.

Looking more closely, a histogram of the values themselves looks like a Negative Binomial distribution. Fitting the curve works out fairly nicely.


This shows how many ballot boxes reported a certain range of votes for Ahmadinejad. The red line is a Negative Binomial distribution fit to the data.

It's not clear what effect sizing will have on the pattern of 2nd digits. But one way we can examine this would be to simulate counts from the negative binomial distribution, estimated from the data, run a lot of different simulations of possible ballot box results, and see what the range of 2nd digit distributions is. Over all these simulated universes, we can figure out 95% confidence intervals, where 95% of the time all digits will be within these bounds. We can see the results in the graph below.


This shows the 2nd digits of ballot boxes' number of votes for Ahmadinejad again, but this time with a simultaneous 95% confidence interval around the digits (created from simulating 10,000 election ballot boxes from the negative binomial distribution). 95% of the time, we expect all digits to fall within those bounds (as they do in the actual Ahmadinejad results).

So, from ballot box sizes (and proportions for Ahmadinejad) centered as they seem to be, we are not actually surprised to see a result like this. This is because for this range and distribution of data, the numbers of 2nd digits are not exactly as predicted by Benford's law (although they show a similar effect).

I'll also note that a more realistic model would be to model the number of people voting in each ballot box area, as well as the distribution of proportion of people voting for Ahmadinejad, rather than modeling the distribution of number of votes for Ahmadinejad directly. I strongly suspect that this would simply result in greater variance (and so larger intervals), but it would be interesting to see.

Benford's Law on District-level Results

Professor Mebane also examined the second digits of the district-level results. While they do have a fair bit of variance, because there are not that many districts, the variance seems in the range of what we would expect; it does not appear to be statistically significant.




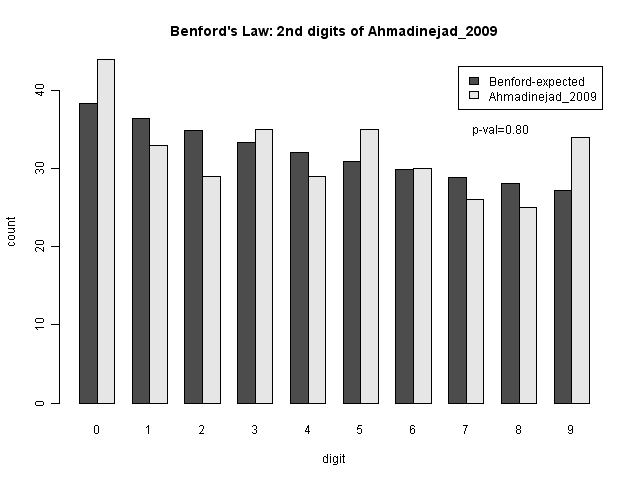
Is Something Strange in the Last Digits? (Scacco and Beber)

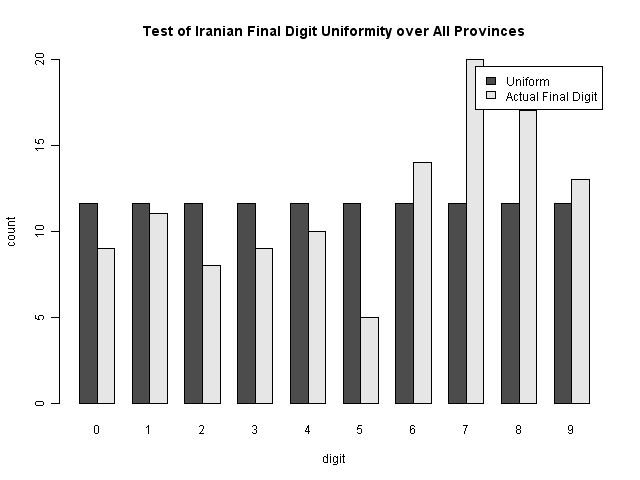
Scacco and Beber wrote an editorial in the Washington Post regarding the frequency of the last and next-to-last digits in the election results. They say that at the province level, the final digits are suspicious. This is because, in a fair election, one would expect the final digits to be essentially random--an equal chance of any final digit. While their probabilities are significantly affected by the use of multiple tests (making their initial claims about final digit significance and final claim of a p-value < .005 disingenuous; Alchemy Today also takes issue with their probabilities), the method is interesting (particularly when considering the plausible vote fraud story they tell).

So let's take a look: their first claim, that the last digits are significantly different from expected, is not quite as strong as they indicate. While it is different from uniform, there are only 116 values. It's expected that some of these will be different; if you perform a Chi-squared test, the p-value is only 0.08--meaning it should happen about 8% of the time; a little unusual, but not damning.


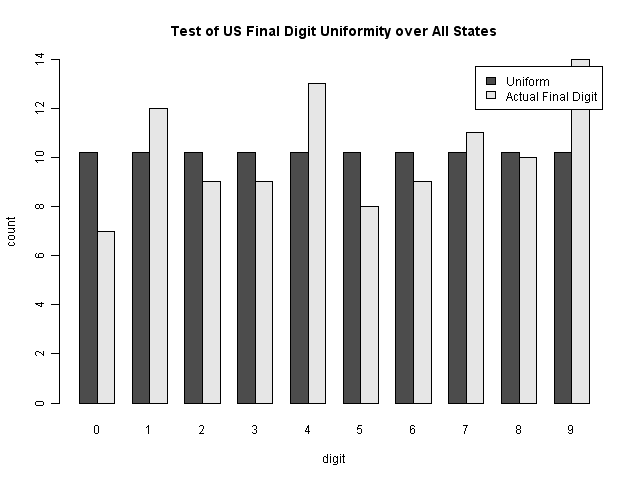
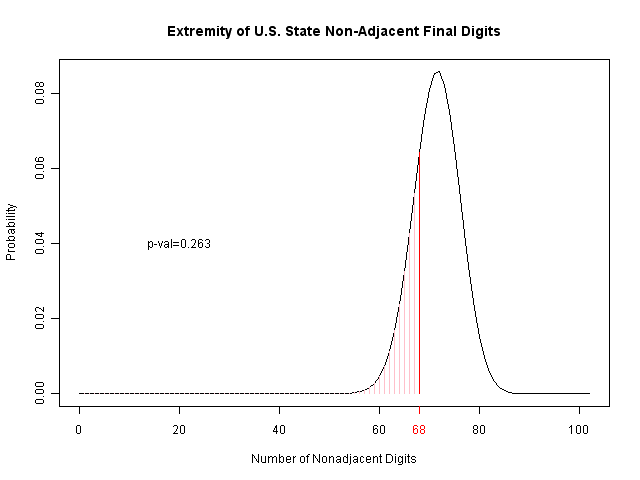
We can further compare this to the results from the latest U.S. election, by state. You can see that this also has some visible discrepancies (though the p-value is 0.878).


Their analysis of the final two digits is more interesting, as it is motivated by the psychological studies showing that humans tend to pick adjacent numbers. However, they also consider 09 and repeated numbers (like 44) to be adjacent; I haven't looked into the psychological literature, but it's not clear this is fully justified. Regardless, you can see the results below. The number of nonadjacent values is marked in red, and the area of probability (for this few or fewer) is indicated in pink to the left. By comparison with the U.S., we may also see that this is suggestive of a problem, but again is not so strong as to be certain.

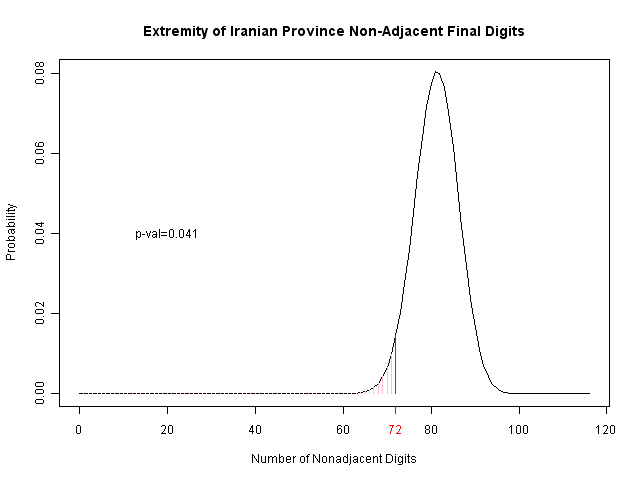
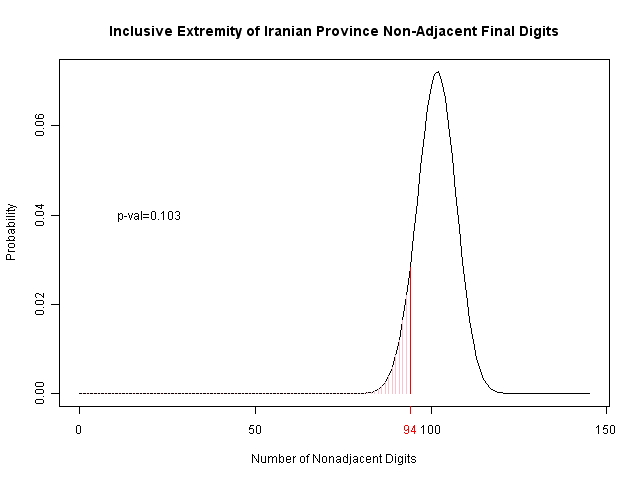This is certainly a little bit unusual; however, we have to recognize that in their analysis, Beber and Scacco chose to remove the invalidated counts by province...if you consider all the province-level counts, the p-value goes up to just over 0.1, which is not very significant.

One could also make the argument that there's no need to have fabricated the invalidated votes...but in that case, there's really no need to fabricate results for Karoubi or Rezaei either; performing the analysis simply on Mousavi and Ahmadinejad's district-level results gives us a p-value of 0.19; not very significant.

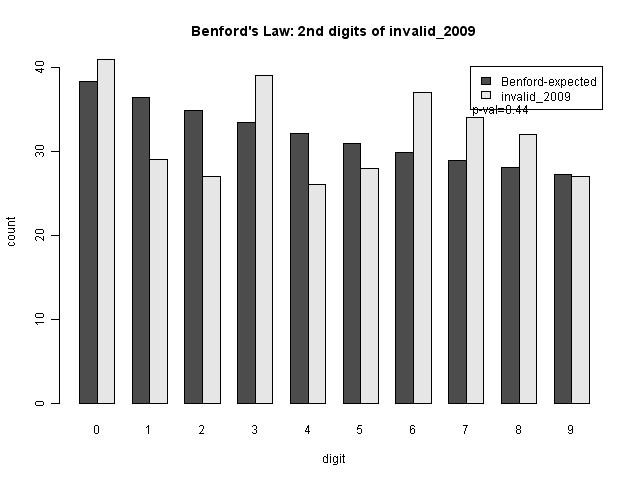
Is Something Strange in the Invalidated Ballots? (Mebane, Lotze)

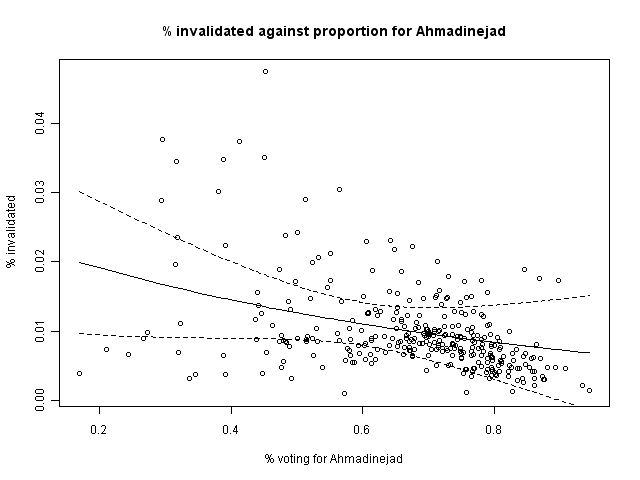
I was curious about whether there might be a relationship between the percentage of votes which were invalidated, and the percentage of votes going to Ahmadinejad. If there were, it could indicate a strategy of greater strictness in areas where Mousavi is favored (thus eliminating a greater number of Mousavi votes). From a simple scatterplot, it appears as though there might be a correlation. Fitting a model, there even seems to be statistical significance (that areas with a higher proportion of votes for Ahmadinejad had a lower proportion of invalidated votes). I've included the best-fit line and 95% CI from the model in the scatterplot.

So, there looks to be an effect, but not a big one. The effect could be due to conscious effort to reject ballots not favoring your preferred candidate, but it could even be an unconscious preference. It could even be that there's some third correlating factor which is influencing both the proportion invalidated and the proportion voting for Ahmadinejad. Even if there was a significant effect on invalidating ballots, it would not have made much of a change in the results--the number of invalidated votes is only about 4% of the difference between Mousavi and Ahmadinejad (and only 8% of that needed for force a runoff).

Professor Mebane also followed up with hus own analysis of invalid ballots, and in particular their relationship to the expected mean second digit, for each candidate. In particular, using R's sm to model the mean second digit using the proportion of invalid votes as a predictor. However, as with the 2nd digit results above, it's not clear to me that the second digit patterns are abnormal--and it seems a strange mechanism to have certain invalid proportions indicate a higher probability of fabricating vote counts (which the 2nd digit test is presumably testing--though professor Mebane indicates that he is using it specifically for ballot box stuffing).

Are there Suspicious Outliers?

One of the most difficult ways to show fraud is to show that the results (in terms of numbers voting for Ahmadinejad) are so much higher than predicted, that they are obviously fake. To make this argument compelling, you have to be able to model what you expect the vote results to be--and this is an extremely difficult problem, in Iran or in other countries.

Mebane attempted to find a model for the percentage voting for Ahmadinejad in 2009. He actually tried a variety of models, including a simple model of the 2009 votes alone, assuming that the percentage of votes for Ahmadinejad is constant across all districts; he also considers a more complex model which uses the first-round results from 2005 as well as the final round 2005 results. Here, we are examining the model which estimates the percent voting for Ahmadinejad, based on:

  • the percentage of people voting for Ahmadinejad in the final round of 2005 voting
  • the ratio of turnout in 2009 to the turnout in 2005

The rationale for the second predictor is that in 2005, there were wide election boycotts; the thought is that those districts with significant boycotts have less support for Ahmadinejad.

Details on this model (a robust overdispersed binomial model) are described in his paper here. (Performing a standard binomial glm on the same predictors provide a similar pattern of residuals.) After fitting the model, we can see what the model's prediction is for each district and compare it to the actual percentage for Ahmadinejad, displaying the differences from the model. In the following graph, we see the predicted value from the model on the X-axis, and the error on the Y-axis. Larger errors mean that Ahmadinejad received more votes in that province then the model would predict; low values mean he received fewer. In fitting this model, the algorithm also identifies outliers, points which are not well-fit by the model. He distinguishes between outliers (districts which are completely left out of the model due to lack of fit) and downweighted districts (which have less influence on the final model). In the following graph, each district is colored with yellow for downweighted items, or red for outliers.

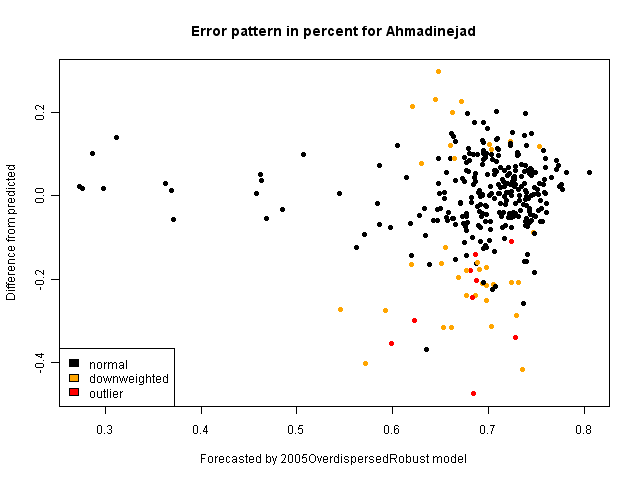
There doesn't seem to be a significant pattern to the outliers: that is, there doesn't seem to be an indication of fraud.

Professor Mebane also analyzed the precinct-level results using a model which uses the first-round 2005 results and second-round 2005 results to predict the 2009 results. In doing so, he finds a high number of precincts with results which do not fit the model, and finds that 2/3 of these have higher-than-expected votes for Ahmadinejad. However, that model seems brittle--the anomalies found seem to simply be the result of the model not fitting the data well (and using a high number of parameters) rather than actually being indicative of fraud in those specific precincts.

In looking at outliers, one would really like to say that the results are very different from what they should be: that the proportion of votes for the candidate clearly does not reflect the population's actual votes. Unfortunately, predicting votes is a very difficult thing--we can see this even in the United States, where the 2008 Democratic primary provided a number of "upsets" between Barack Obama and Hilary Clinton, where the actual outcome was not expected to be possible. The truth is that people's votes are affected in ways that are difficult to measure, and can change in unexpected ways. In order to make an outlier argument, you have to be able to predict the votes with some degree of accuracy, and to know what that accuracy is; right now, I don't think there are any models which can claim this.

Is the Boycott Effect Real? (Mebane)

This is not so much a question of fraud as one about voting patterns between 2005 and 2009. In 2005, there was a significant movement to boycott the elections, as they were seen as simply a way for the regime to legitimize its authority while repressing any real opposition. So one would expect to see that in 2009, those places with large increases in turnout to also show a lower proportion voting for Ahmadinejad (because the increase would often be due to voters who had boycotted in 2005).

As indicated by the model above, it seems like several districts did indeed have an impact due to vote boycotting in the 2005 elections. This plot shows the 2005 turnout (on a log scale) against the 2009 turnout (also on a log scale), with each item colored by the proportion voting for Ahmadinejad. One can see a number of smaller provinces on the left, which had much higher turnout in 2009 than 2005 and also tended to vote more heavily against Ahmadinejad.

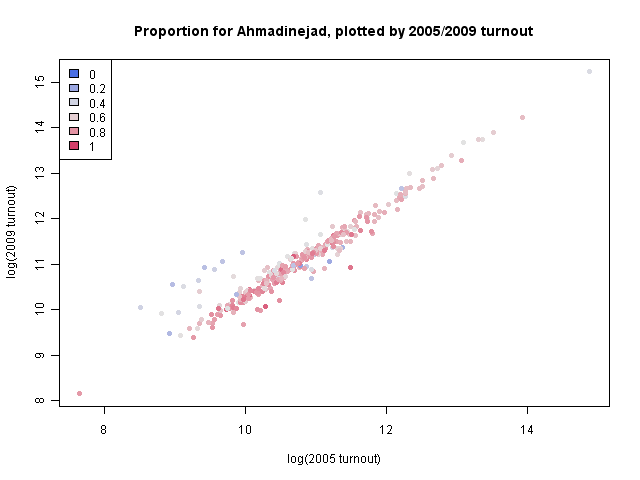
Turnout being affected by previous boycotts in this way can also help to explain the turnout changes noted by the Chatham House analysis.